Computer and the Brain | Book Review Part 1

John Von Neumann, a Hungarian-born scientist is argued to be the greatest thinker of the 20th century. I am assuming a low chance that you have not heard of his name before if you are reading this.

Before the Computer and The Brain was written, the fields of neuroscience and computation were separate, and this book marks the earliest serious merge of the two fields. It is widely accepted that the brain-inspired the design of computation, and the intuition at play here is what's amazing about it. Using the physics concepts to theory craft and implement in another field.

In the 1950s, the machines were not so great yet great scientists were sure the level of technology and intellectual tasks done by machines was only going to get better. Stanislav Ulam , a Polish Mathematician, Physicist, and Computer Scientist who also worked on the Manhattan Project with Von Neumman and had regular conversations together…

It was Von Neumman who first discussed technological “singularity” originated from the event horizon singularity discussed in physics focused on black holes where the sciences as know them break apart, and no definitive rules are governed.

Technological singularity is a theory where machines are put by us, or by themselves into an ever-lasting loop of self-improvement. Ulam noted as follows in his writings:

One conversation centered on the ever accelerating progress of technology and changes in the mode of human life, which gives the appearance of approaching some essential singularity in the history of the race beyond which human affairs, as we know them, could not continue.

Von Neumann:

He was in short involved in the field of physics, quantum mechanics, math, game theory, chemistry, nuclear power, computer programming and architecture, and robotics. The The Innovators book by Walter Isaacson, describes him like a bee, pollinating each different field with his intuition. If you are questioning whether he had contributed to the field you are studying/ or professing … yes he was probably there.

The book I will give a detailed summary of with my commentary to the best of my ability. His studies on this topic were cut short as he was dying from bone cancer which affected him physically and mentally. He had already contributed so much to other sciences before and got very deep into the intersection of computer science and neuroscience here.

We will cover chapter one here titled “The Computer”. I will cover the second chapter titled “The Brain” hopefully in a few weeks.

The book is not an easy read and is analytical heavy which might be hard for some readers. Because I admire his intellect and his ability to contribute to so many fields I wanted to write about it and challenge myself. I am choosing this contribution of his mainly because it also aligns with my current interest that being neuroscience. Lastly, I take responsibility for the explanations I will be making here as it was not an easy reading material for me.

Part 1: The Computer

Existing computers at the time fell into analog and digital at the core. Analog and digital systems operate on continuous and discrete spaces respectively.

Continuous System:

An example of a continuous system is acoustic drums , where the sound is produced by the physical vibrations of a drumhead when struck creating resonance. These vibrations create continuous sound waves, where the intensity, and frequency depend on where you hit it and give you a smooth sound.

Discrete System:

On the contrary, a discrete system is represented by electronic drums, which work by triggering pre-recorded digital samples when you hit the pads. The electronic system then processes and outputs discrete sound events, which limits the continuous variability.

Analog Computation:

Numbers are stored here in continuous form like the voltage, current, or mechanical motion. The 4 basic operations of arithmetic (addition, subtraction, multiplication, division) can be done by manipulating currents.

In some other analog computers, mechanical motion is at play and it's called the differential analyzer. The same 4 basic operations are implemented with the differential gear to calculate: $(x\pm y)*0.5$

For multiplication, the integrator is used, and the inverse with some tricks will give you division. Remind you, that we are still working with continuous numbers in this example also. The operations $(x\pm y)*0.5$ and the integrator in this example are also more viable than the arithmetical ones. The book claims having the exact implementation of the 4 basic arithmetic operations would not be economically viable.

Digital Computation:

We are now talking about the binary system of arithmetic and how we encode our base-10 to base-2 and represent it in a sequence of decimal digits in the computer. A marker is most similar to a digit. At the time Von Neumman wrote it, it was referred to as the decimal marker system, you might know it as the binary system.

• 1 marker → 1 combination (0, 1)
• 2 markers → 4 combinations (00, 01, 10, 11)
• 3 markers → 8 combinations (000, 001, 010, 100, …, 111)
• 4 markers → 16 combinations (0000, …, 1111)

I will not dive deeper into how the encoding is done from base-10 to base-2. The main point is numbers are stored discretely.

For example, to represent a select group of characters like below, you need 8 markers giving you 2⁸=256 combinations, 80 of which to use.

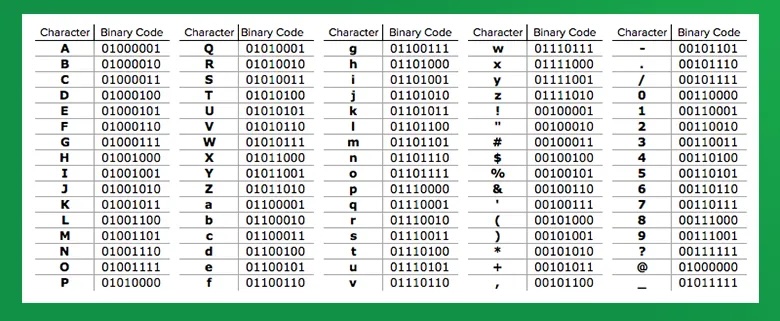
Fundamentals:

Parallelization:

For example, we have a 735.829, a 12-digit number, each digit represented by groups of 4 markers (because with only four markers can we represent the first 10 numbers, hence we need 4 times 12 = 48 channels to have the information readily available in other parts of the computer. By representing numbers in the discrete space, we can benefit from parallelization. Von Neumann doesn't mention analog systems and parallelization likely because it wasn't so common due to difficulties of working with continuous signals like signal degradation which would cause your computer to be out of sync precision-wise between different parts.

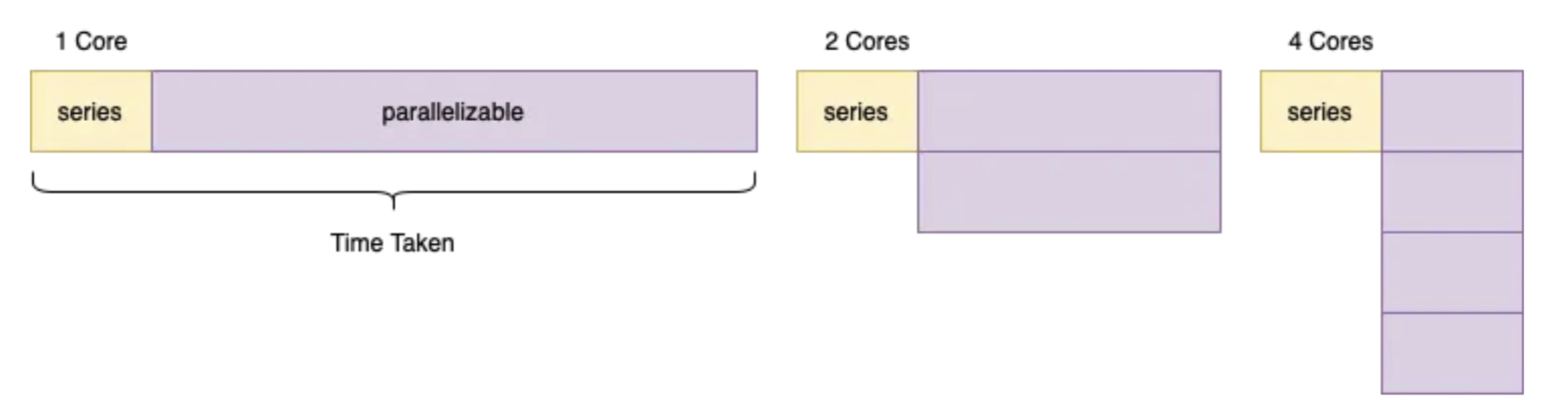
Ideally, we want to use parallelization when a task is near 100% parallelizable (divide the tasks and the tasks are independent of each other’s outcomes) to speed up computation. Today parallelization is widely used for processing large datasets under time constraints and running ML or DL models for inference stage using HPC platforms(High-performance computing). Amdahl’s Law is a simplification of how much speedup we can get.

It essentially separates the tasks into a series portion and a parallelizable portion. We can only apply parallelization for the second part. The formula essentially shows that speedup is limited by the portion of the task that remains serial.

Implementing the Basic Operations:

We will not dive deep into binary arithmetic concerned with addition, subtraction, division, and multiplication that are done in digital computers. The point is, that the implementation and theory of these operations are very different than analog systems and operate discretely.

If you were to command the computer to carry out these basic operations on an analog computer, you would need “enough” organs. For the digital computers we are talking about, the principal idea is the four basic arithmetic operations are carried by only one organ and one is enough. Of course, you can use multiple at once to increase performance, but we are not concerned with this, but with functionality.

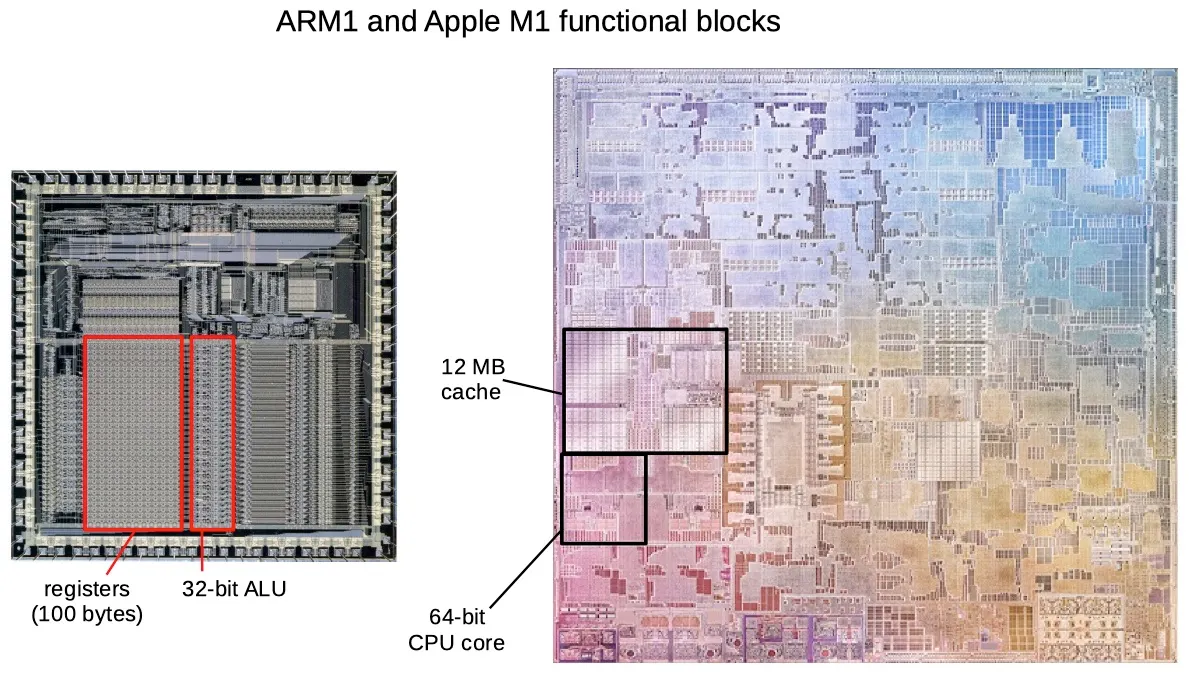
Today the ALU (Arithmetic Logic Unit) organ is responsible for that. The following example is Apple’s M1 2020 CPU architecture looking at the 32-bit ALU (32-bit or markers precision for basic arithmetic).

Memory:

Like you need a workspace to place your books, laptop, coffee, or tea, you need a physical space inside a computer. In other words, to carry out the basic operations you need memory where you store calculations and your planning i.e. order of your work. In the example of your workspace, you can have multiple tables at once and people working on them, and for a computer, you can have multiple memory organs thus increasing the capacity of work to be done. To identify which table to work on we need the address and we assign numbers uniquely to each different memory space/register. Similar to addressing memory registers, we can assign a unique address to each basic arithmetic operation. To carry out the work, you need to just order the processing of operations and on which memory registers.

While ordering tasks, you can decide to include branching (if else statements introducing the concept of “states”) and can also transfer information from one memory register to another called a “successor”. If the transfer is done via branching it is called “conditional transfer”. Any computation that you want to carry out at the end can be represented by a sequence of decimal digits and stored inside the initial memory register. Planning and execution are finally interlinked.

Precision:

Because there is a limit to how much memory we can have, there is the problem of precision, i.e. percentage of the original knowledge we can keep.

Let's say you want to measure the length of a snake that is exactly 1000 meters. and computer that at core measures 1 meter, with a precision of 1:10³ would essentially have a margin of error +-1, because 10³ is roughly its limit.

At the time the Computer and the Brain was written, analog and hybrid (electrical-analog) computers would have a precision of at most 1:10⁵. So measuring a 1000-meter snake would have an error rate of 0.001 or 1 centimeter. For digital like the modern computers we have today, it was 1:10¹² (+- 1 nanometer).

So why do we need higher precision? Or do we need higher precision? For most day tasks 1:10³ precision is enough, for scientific tasks like aerospace, quantum physics, or molecular biology, the required precision can go up to 1:10⁹. I can personally give an example from a competition about processing exo-chemistry satellite data of exoplanets. Yes, it is very niche.

Today, precision has numerous formats. IEEE standard is the house of few formats. In IEEE 754 for example the 32-bit format looks like follows:

We essentially have to store. Essentially there is a formula for it, but we don’t need to get deep any further.

• One bit for the Sign (+ or -) either 0 or 1 respectively.
• Eight bits for Exponent (exponent = stored_exponent -127)
• 23 bits for Fraction / Mantissa (a leading leftmost 1 bit is implied → 24-bit precision)

Like 32-bit, there are 64-bit, 128-bit, or 16-bit formats too. Essentially, when we do arithmetic operations we want to minimize rounding errors that accumulate over time.

Speed:

The speed factor depends on how fast you can access memory . Since we talked about multiple memory registers, they can be also layered hierarchically.

Access time increases exponentially as you get deeper down the hierarchy but the size also increases. So there is an inverse relationship between access time (speed) and the size of the memory register we want to access. Today accessing RAM takes about 10 nanoseconds, and Von Neumann provides access times of some present at his time …

• Ferromagnetic core memory: 5 to 15 microseconds
• Electrostatic memory: 8 to 20 microseconds
• Magnetic drums: 24 to 3 milliseconds
• Magnetic tapes: 14 microseconds per line (words are 5 to 15 lines)

Modern architecture now uses hard disks at the bottom layer, much more resilient to motion than magnetic tapes.

The memory architecture is but an approximation of what a good working flow would look like in the dumbest possible way that a machine can comprehend. It kind of shows that when things are dumbed down so much the impact it generates is unexpectedly impressive.

Software-level speed:

Although not mentioned, Software Engineers today are concerned with optimization i.e. speeding up computation that can be done at the software level. Big O notation is one example. Depending on the type of programming language, some are closer to hardware, and the closer, the faster. But generally, you can use Big O as a reference for each language.

Big O is nothing new, so I will not go deep here either. Just know that the input i.e the prior knowledge you provide to the computer significantly impacts the runtime / execution time (the time it takes to finish the task).

With given hardware, you can also optimize the software and improve speed. SO speed is not only dependent on the hardware available. Remember that Appolo 11 space mission software was small. It had 2,048 words, 32,768 bits of RAM (4.096 KB) + 589,824 bits of read-only memory (72 KB) and it ran on 0.043 MHz processor (CPU).

The below image is 80 KB for reference.

Thank You

This has been the summary and some of my commentary on the first chapter. Lastly, before finishing off I want to share an interview recorded by his colleague Edward Teller.